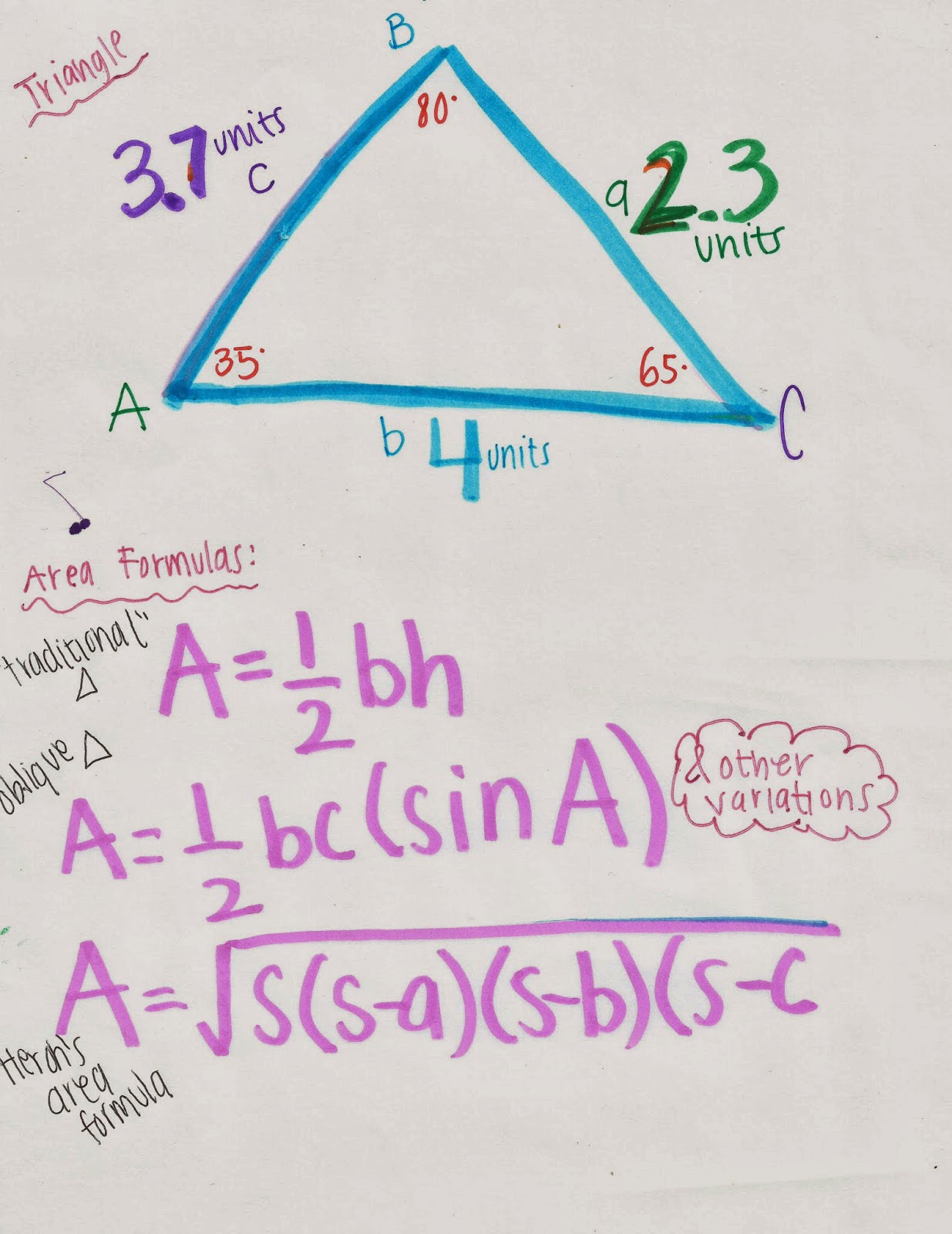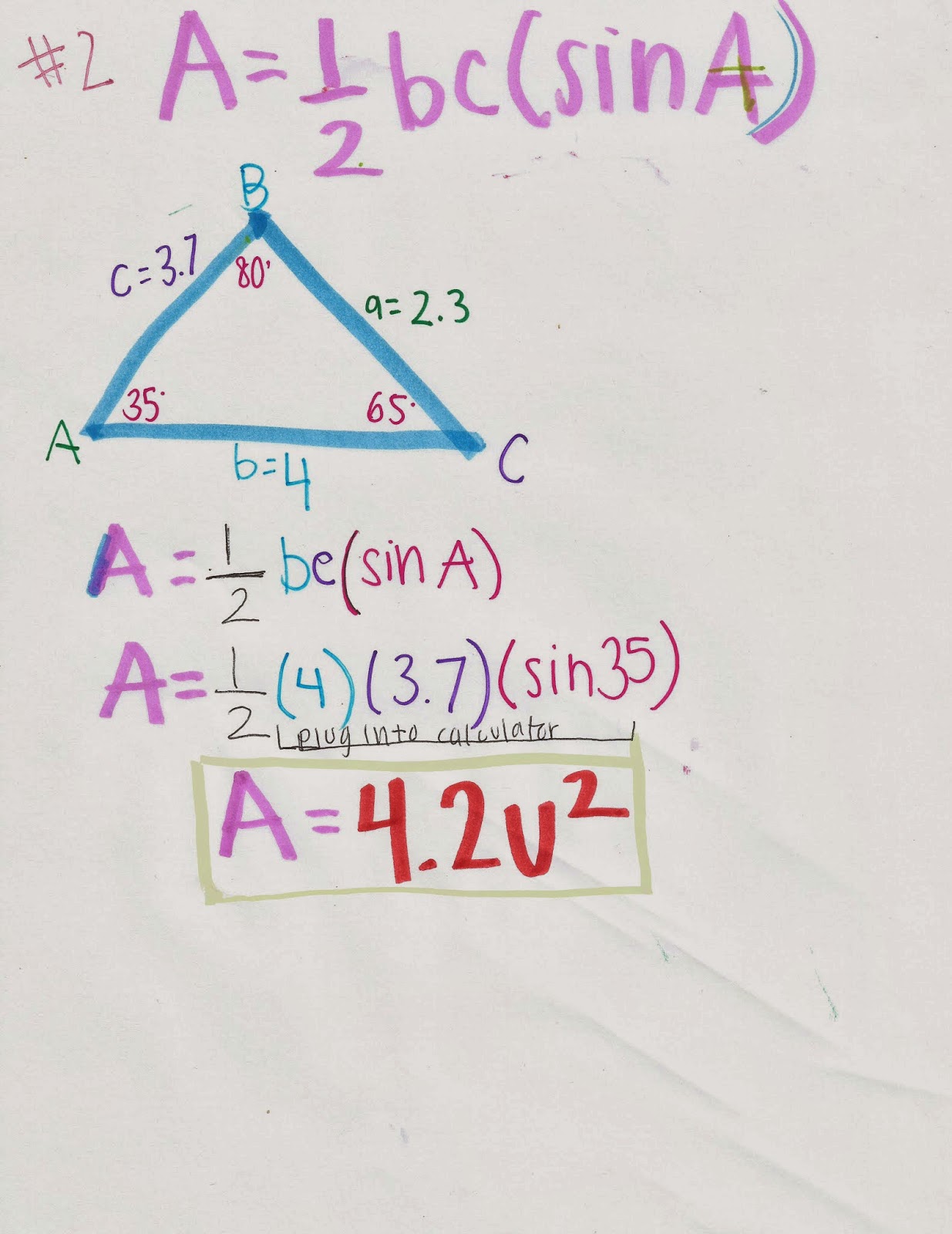SP #7: Unit Q Concept 2

This SP7 was made in collaboration with Margie V.  Please visit the other awesome posts on their blog by going here.

Problem

Solutions

1. Using Pythagorean/Ratio/Reciprocal identities (Unit Q Concept 2)

2. Using SOHCAHTOA (Unit O Concept 5)

Although the methods are slightly different, both of the methods led to the same answers. We concluded that we can use both methods to find the values. This proved that the identities deal with SOHCAHTOA.

I/D #3: Unit Q - Pythagorean Identities

Inquiry Activity Summary

1. Where does sin²x+cos²x=1 come from to begin with?


Example with one of the "Magic 3" ordered pairs from the Unit circle.

2.

Inquiry Activity Reflection

1.  The connections that I see between Units N, O, P, and Q so far are all of the concepts deal with triangles or angles of some sort. For example we have worked with right triangles, non-right triangles, obtuse angles, acute angles. For the non-right triangles we had to learn about the Law of Sines and Law of Cosines.  Another connection is that we learned how to utilize sine, cosine, tangent, cosecant, secant, and cotangent along the other units to find missing pieces of information. In addition, all the trigonometry functions related to the unit circle.

2. If I had to describe trigonometry in THREE words, they would be complex, memorization, and concise. 

WPP #13 & 14: Unit P Concept 6 & 7

This WPP13-14 was made in collaboration with Margie V.  Please visit the other awesome posts on their blog by going here.

http://inspirationalstorytellers.com/the-daisy-and-the-oak-tree/

The Problem

a) Danielle is due east from an oak tree. Danielle is looking at Andrew at a bearing of S32W. Andrew is looking at the same oak tree with a bearing of N15E. Andrew is also 52 feet away from the oak tree. How many feet apart are Andrew and Danielle?

b) Andrew and Danielle are now together and they decide to go on a date. They go on a date and now it is time to part. They leave from the same point. Their paths diverge by a bearing of 088 degrees. If Danielle walks for 2.7 miles and Andrew walks for 3 miles, how far apart are they at this time?

The Solutions

BQ# 1: Unit P Concepts 1-5

1. Law of Sines: In the Law of Sines, a proportion is set up and you can find an angle or a side of a non-right triangle. The Law of Sines works when you have the angle-side- angle triangle, angle-angle-side triangle, or side-side-angle. The pictures below will show how the Law of Sines is derived.

5. Area Formulas: The area formulas for non-right triangles are shown below with the angles of 35*-65*-80* and a base of 4. You will get the area to be 4.2 units squared for all three area formulas.

a)Using the "traditional" area formula:

b) Using the area of an oblique triangle:

c) Using the Heron's formula:

WPP #12: Unit O Concept 10: Angles of Elevation and Depression

http://gomighty.com/wp-content/themes/gomighty/lib/goal_images/files/Hot-Air-Balloon.jpg

The Problem

a) Andrew is at ground level and measures the angle of elevation to the hot air balloon to be 37*. If, at this point he is 57 feet away from the hot air balloon, what is the height of the hot air balloon from the ground? (round to the nearest foot)

b) Andrew is now in the hot air balloon and measures the angle of depression which is 25*. Andrew knows that he is 240 feet high up in the air than the base of the forest. How far away horizontally is Andrew from the forest? (round to the nearest foot)

The Solutions

I/D #2: Unit O: Derive the Special Right Triangles

Inquiry Activity Summary

Derive the 45-45-90 triangle from an square with a side length of 1

Derive the 30-60-90 triangle from an equilateral triangle with a side length of 1

Inquiry Activity Reflection

Something I never noticed before about the special right triangles is where the triangle comes from. I did not know that the 45-45-90 degree triangle came from a square and that the 30-60-90 degree triangle came from half an equilateral triangle. It was interesting to find out that so much can be found with the Pythagorean Theorem.

Being able to derive these patterns myself aids in my learning because if I forget the rules for the special right triangles I will be able to derive them from a square and the equilateral triangle with the side lengths of 1. I also will know how to use the Pythagorean theorem to determine the side and substitute the values for the variable n, so any other multiples of those values can be used.